Pembuktian tidak langsung lainnya adalah pembuktian dengan kontradiksi. Metode pembuktian ini agak berbeda dengan kedua metode pembuktian sebelumnya, pada metode pembuktian dengan kontradiksi ini kita mencoba mencari kesalahan logika (kontradiksi),baik kontradiksi dengan fakta (misal: 1 = 0) maupun kontradiksi dengan hipotesis yang dimiliki. Struktur logika pada metode pembuktian ini adalah \rightarrow&space;c)
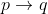 (cek nilai kebenaran kedua pernyataan tersebut menggunakan tabel kebenaran). Salah satu keuntungan dari pembuktian ini adalah kita mendapatkan tambahan hipotesis sebagai modal dalam melakukan pembuktian.
(cek nilai kebenaran kedua pernyataan tersebut menggunakan tabel kebenaran). Salah satu keuntungan dari pembuktian ini adalah kita mendapatkan tambahan hipotesis sebagai modal dalam melakukan pembuktian.
Kita memulai pembuktian dengan menggunakan 2 hipotesis yakni: hipotesis awal ) dan negasi dari kesimpulan
dan negasi dari kesimpulan ) sedemikian rupa sehingga dengan langkah-langkah yang tepat kita sampai pada kesimpulan yang akan didapatkan merupakan kontradiksi (baik kontradiksi dengan fakta maupun kontradiksi dengan hipotesis yang dimiliki). Bila dibuat strukturnya, maka pembuktian dengan kontradiksi memiliki struktur sebagai berikut:
sedemikian rupa sehingga dengan langkah-langkah yang tepat kita sampai pada kesimpulan yang akan didapatkan merupakan kontradiksi (baik kontradiksi dengan fakta maupun kontradiksi dengan hipotesis yang dimiliki). Bila dibuat strukturnya, maka pembuktian dengan kontradiksi memiliki struktur sebagai berikut:
……
|
Pernyataan logis
|
Diakhiri: kontradiksi (c)
Teladan 1.3.1: Misal  merupakan anggota bilangan bulat, jika
merupakan anggota bilangan bulat, jika 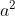 merupakan bilangan genap maka
merupakan bilangan genap maka  merupakan bilangan genap.
merupakan bilangan genap.
Bukti: Berdasarkan hipotesis maka 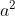 merupakan bilangan genap, hipotesis berikutnya (negasi kesimpulan) andaikan
merupakan bilangan genap, hipotesis berikutnya (negasi kesimpulan) andaikan  merupakan bilangan ganjil. Berdasarkan pengandaian maka terdapat k anggota bilangan bulat sehingga berlaku
merupakan bilangan ganjil. Berdasarkan pengandaian maka terdapat k anggota bilangan bulat sehingga berlaku 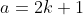 .
.
Sehingga nilai ^{2}=2\left&space;(&space;2k^{2}+2k&space;\right&space;)+1) , bila terdapat
, bila terdapat  merupakan bilangan bulat dan
merupakan bilangan bulat dan 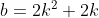 sehingga berlaku
sehingga berlaku 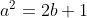 .
Kesimpulan yang didapat adalah
.
Kesimpulan yang didapat adalah 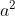 merupakan bilangan ganjil, hal tersebut bertentangan (kontradiksi) dengan pengandaian bahwa
merupakan bilangan ganjil, hal tersebut bertentangan (kontradiksi) dengan pengandaian bahwa 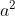 merupakan bilangan genap.
Sehingga pernyataan “Misal
merupakan bilangan genap.
Sehingga pernyataan “Misal  merupakan anggota bilangan bulat, jika
merupakan anggota bilangan bulat, jika 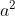 merupakan bilangan genap maka
merupakan bilangan genap maka  merupakan bilangan genap” terbukti benar.
merupakan bilangan genap” terbukti benar.
Teladan 1.3.2: Misal dan
dan  merupakan anggota bilangan bulat, jika
merupakan anggota bilangan bulat, jika  dan
dan  merupakan bilangan genap maka
merupakan bilangan genap maka 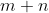 merupakan bilangan genap.
merupakan bilangan genap.
Bukti: Berdasarkan hipotesis maka bilangan genap dan
bilangan genap dan  bilangan genap hipotesis berikutnya (negasi kesimpulan) andaikan
bilangan genap hipotesis berikutnya (negasi kesimpulan) andaikan 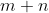 merupakan bilangan ganjil.
Bila
merupakan bilangan ganjil.
Bila  dan
dan  bilangan genap maka terdapat
bilangan genap maka terdapat  dan
dan  anggota bilangan bulat sehingga berlaku
anggota bilangan bulat sehingga berlaku 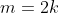 dan
dan  .
Sedangkan bila
.
Sedangkan bila 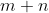 merupakan bilangan ganjil maka terdapat
merupakan bilangan ganjil maka terdapat  anggota bilangan bulat sehingga berlaku
anggota bilangan bulat sehingga berlaku 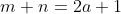 .
.
Berdasarkan hipotesis pertama (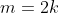 dan
dan  ) dan kedua (
) dan kedua (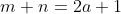 ) dapat pula ditulis
) dapat pula ditulis 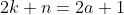 atau
atau +1) .
Bila terdapat
.
Bila terdapat 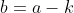 yang merupakan bilangan bulat, maka nilai
yang merupakan bilangan bulat, maka nilai +1=2b+1) .
Kesimpulan yang didapat adalah nilai
.
Kesimpulan yang didapat adalah nilai 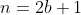 yang berarti
yang berarti  merupakan bilangan ganjil, hal tersebut bertentangan (kontradiksi) dengan pengandaian bahwa
merupakan bilangan ganjil, hal tersebut bertentangan (kontradiksi) dengan pengandaian bahwa  merupakan bilangan genap.
Sehingga pernyataan “Misal
merupakan bilangan genap.
Sehingga pernyataan “Misal  dan
dan  merupakan anggota bilangan bulat, jika jika
merupakan anggota bilangan bulat, jika jika  dan
dan  merupakan bilangan genap maka
merupakan bilangan genap maka 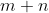 merupakan bilangan genap"terbukti benar.
merupakan bilangan genap"terbukti benar.
Teladan 1.3.2: Misal
Bukti: Berdasarkan hipotesis maka
Berdasarkan hipotesis pertama (